In this post we will take a look at a domain-specific language (DSL) for creating interactive and composable animations. At its core, the DSL is based on an effect handler (or free monad) approach with a slight twist. In addition to the bind and return combinators, we need a parallel combinator. We will take a look at some basic use cases and how the DSL is built from the ground up.
History
The DSL I will present in this post originated as a layer I created on top of tweening functionality provided by the Phaser game engine. By the way, the word tweening is short for inbetweening, which means: generating frames inbetween two images to create the appearance of motion. Anyway, the tweening API in Phaser provides the user with the ability to alter properties of objects over time. For example, let’s say we start with an object obj = { x: 100, y: 100 }. Then, we can attach a tween on obj, for example the tween object tween.to({ x: 150 }, 200). By attaching this tween to obj, it will increase the property obj.x to 150 over the next 200 ms. There are various configuration parameters, such as different easing functions, to create all kinds of basic animations.
I use this to create various animations within a game prototype I am working on. The game features abilities with multiple effects which happen in sequence. When such an ability is activated, the animation for each of these effects needs to play in order. An animation for an effect can consist of various other animations in parallel. And what makes things even more complicated are statuses which intercept and alter effects, again with corresponding animations. This means that there are tons of animations that need to play in sequence or in parallel, and these are in turn composed of multiple animations playing in sequence or in parallel. Specifying this with the basic tweening interface was quite cumbersome, and so I started experimenting with this DSL on top of the more basic operations and have been very happy with it so far.
Now I want to take it a step further by porting the DSL to Haskell and looking at it from an effect handler perspective. We will be looking at the current iteration of the Haskell DSL in this post.
Overview
First, let’s take a look at the very basics we want to achieve with the DSL: composing basic animations in sequence and in parallel. The post leaves out some code, but you can find the full example code in this github repo.
Basic Animations
As a first step, we need to specify what a basic animation is. We will model a basic animation consisting of three things. First, its duration specifies how many seconds the animation should last. Second, we provide a way to specify which values in our world model should change, we do this by passing a traversal since we can potentially focus on multiple values. Last, we provide the wanted target value, which tells us what the values focused on by the traversal should be at the end of the animation.
Note: Traversals are a concept from the various lens libraries. I will not go into detail on lenses in this post. I hope the use of lenses in this post is lightweight enough to understand from context what is going on even if you are not familiar with them. If you do want to read more about this, maybe this lens tutorial can be of help.
Let’s say we want to create the animation of a box moving over the x-axis, we would create it as follows. We create a basic animation with a duration of 0.2 seconds, a traversal focusing on sprites.box.x, which is the x-value of the box object in the sprites of our world, and an end value of 50.
basicBoxAnim = basic (For 0.5) (sprites . box . x) (To 50)
This results in the following animation. Obviously, we are still missing some code to actually create these animations, but this gives an idea of what we are working towards.
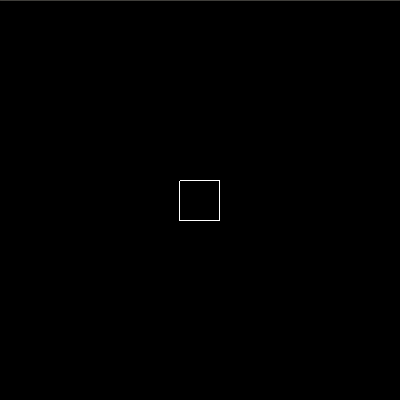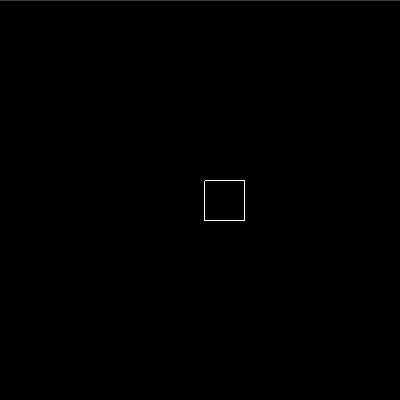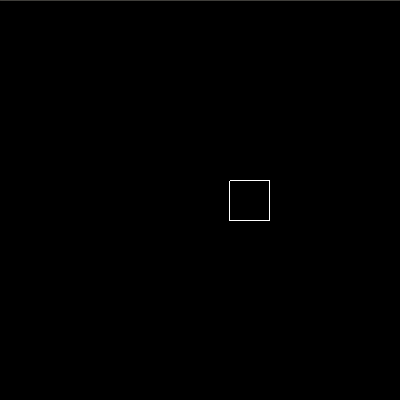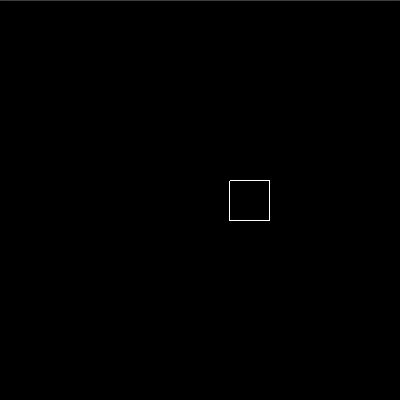
Sequential and Parallel Animations
The next steps in our DSL are sequential and parallel composition of animations.
First, let’s take a look at sequential composition. With the seq combinator, we can create an animation which consists of multiple basic animations executed sequentially. For example, if we wanted our box to walk a square path, we can create this by first creating an animation which increases the x value, then increases the y value, then decreases the x value and lastly decreases the y value. This animation is shown by means of code and a visual animation below.
seqBoxAnim = seq
[ basic (For 0.5) (sprites . box . x) (To 50)
, basic (For 0.5) (sprites . box . y) (To 50)
, basic (For 0.5) (sprites . box . x) (To 0)
, basic (For 0.5) (sprites . box . y) (To 0)
]
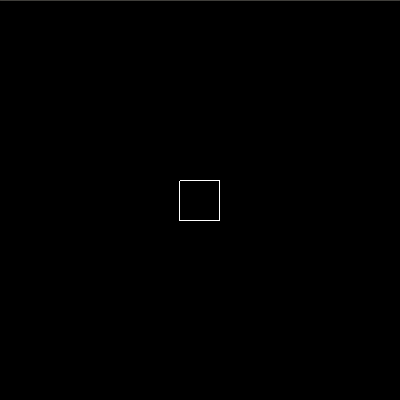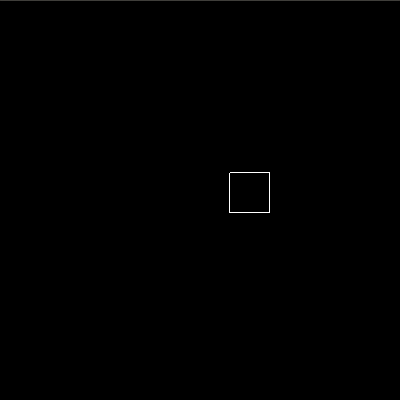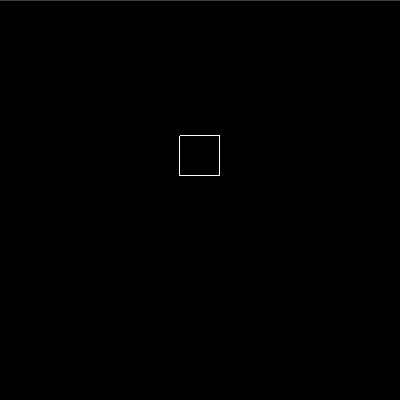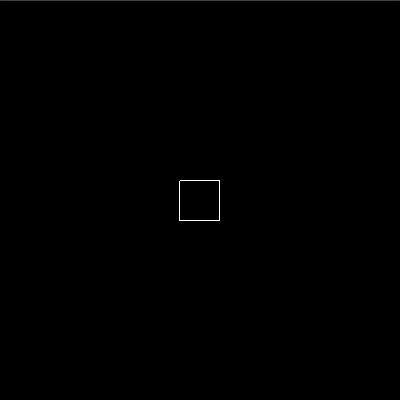
We can also compose animations in parallel with the par combinator. For example, to create an animation of a box moving diagonally, we compose an animation of increasing x and increasing y in parallel. The code and visual are given below.
parBoxAnim = par
[ basic (For 0.5) (sprites . box . x) (To 50)
, basic (For 0.5) (sprites . box . y) (To 50)
]
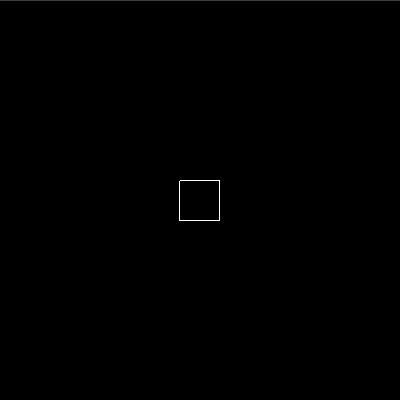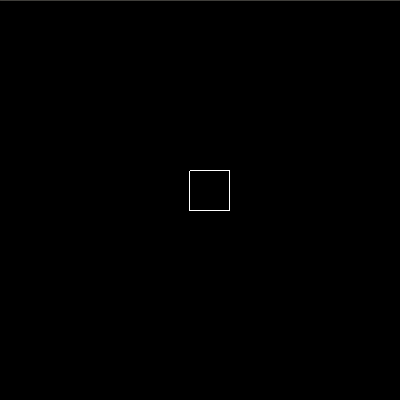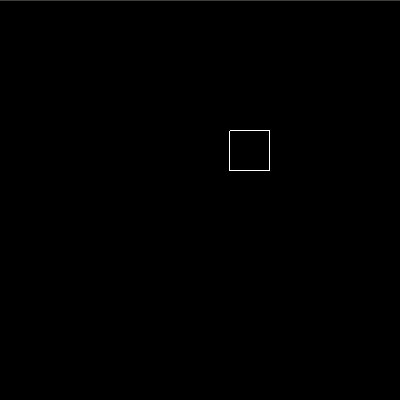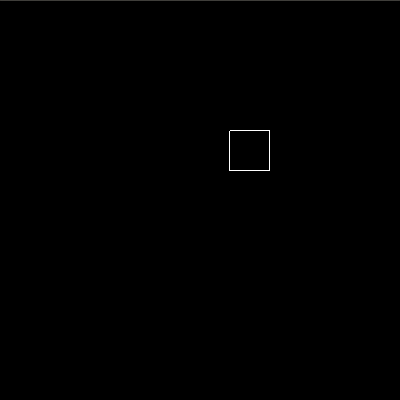
Effect DSL
Now, we will take a look at the internals of the DSL’s and build it from an effect handler perspective. When working in an effect handler setting, DSL’s are divided in two parts: the operations and the combinators. The former are the basic effects supported by our DSL, such as the basic animation effect. The latter represent the possibilities in which effects can be combined to create larger effects, such as the seq and par combinators. However, we will take the more well-known combinators bind and return as starting point, which makes our DSL a free monad.
Starting Point
First, we have only one operation: Basic, which represents the effect of executing a basic animation. Notice that the Ops data type has a type parameter a. This type parameter represents the return type of the operation. The return type of the Basic operation is not very interesting, as it is unit. Later we will see an example with a more interesting return type.
-- duration in s
newtype Duration = For Float
-- end result value of animation
newtype To = To Float
data Ops obj a where
Basic :: Duration -> Traversal' obj Float -> To -> Ops obj ()
Next, we introduce the Bind and Return combinators. The f type parameter is a higher-kinded parameter where we will plug in Ops obj to create our actual DSL.
data Dsl f a where
Bind :: f a -> (a -> Dsl f b) -> Dsl f b
Return :: a -> Dsl f a
Note: Intuitively speaking, this is a free monad because we obtain a free instance for the Monad typeclass. In this post we won’t delve deeper into the mathematical background of this data type. If you are interested in this, the free package is a good starting point.
The return type of an operation is of importance in the Bind combinator. It takes as input an f a, or an effect from the operations f with a return type a, and a function a -> Dsl f b, the remaining part of the effect which has to be executed after we have done the first operation. The Return combinator allows us to embed any value a as a no-op effect.
Creating a sequential animation with this encoding can be done as follows. We create a series of Binds where we put a Basic animation as the first parameter and the remaining effects in the continuation function. These functions have unit as input value, since that is the return type of the Basic effect. So, we can implement the seqBoxAnim example like this:
seqBoxAnim' =
Bind (Basic (For 0.5) (sprites . box . x) (To 50)) $ \_ ->
Bind (Basic (For 0.5) (sprites . box . y) (To 50)) $ \_ ->
Bind (Basic (For 0.5) (sprites . box . x) (To 0)) $ \_ ->
Bind (Basic (For 0.5) (sprites . box . y) (To 0)) $ \_ ->
Return ()
Or, we can implement the seq combinator in a generic fashion. This combinator takes a list of animations and creates an animation which executes them sequentially. This implementation uses the omitted Monad instance for Dsl.
seq :: [Dsl (Ops obj) ()] -> Dsl (Ops obj) ()
seq [] = Return ()
seq (anim:r) = anim >>= (\_ -> seq r)
Combined with the following helper function for the Basic effect, we can then literally implement the first version of seqBoxAnim.
basic :: Duration -> Traversal' obj Float -> To -> Dsl (Ops obj) ()
basic duration traversal to = Bind (Basic duration traversal to) (\_ -> Return ())
Par Combinator
We were able to support sequential animations out of the box with the free monad, but we are not able to support parallel animations. We might expect that we need to add an applicative combinator to our existing monad combinators. However, that only allows us to specify parallel effects (the Ops data type) as opposed to parallel animations (the Dsl data type). In essence, it is the difference between adding this combinator:
ParLimited :: [f a] -> ([a] -> Dsl f b) -> Dsl f b
or this combinator:
Par :: [Dsl f a] -> ([a] -> Dsl f b) -> Dsl f b
Thus, the Par combinator takes as first argument a list of animations to execute in parallel. The second argument is a continuation which expects the return values of each of the animations executed in parallel.
So now our Dsl data type becomes:
data Dsl f a where
Bind :: f a -> (a -> Dsl f b) -> Dsl f b
Return :: a -> Dsl f a
Par :: [Dsl f a] -> ([a] -> Dsl f b) -> Dsl f b
With our shiny new combinator, we can support the first parBoxAnim example.
parBoxAnim' =
Par
[ Bind (Basic (For 0.2) (sprites . box . x) (To 150)) (\_ -> Return ())
, Bind (Basic (For 0.2) (sprites . box . y) (To 50)) (\_ -> Return ())
] $ \_ ->
Return ()
Or, we can implement the par combinator generically, which can again be used in combination with basic to allow the literal implementation of the earlier parBoxAnim.
par :: [Dsl (Ops obj) ()] -> Dsl (Ops obj) ()
par l = Par l (\_ -> Return ())
Running Animations
Now that we know how the DSL is implemented under the hood, we can take a look at how running animations actually works.
Applying Operations
First, we take a look at applying an operation to a world model, represented by the abstract type obj. The second parameter t, a Float, is the amount of time elapsed since the previous frame. The third and last parameter is the operation that we want to apply, of type Ops obj a. The output of the function is a tuple containing the new world model and either a new operation or a result value.
There is only one case to consider, the Basic operation. The function works as follows.
- We update the value(s) within the world model based on the amount of elapsed time.
- We deduct the elapsed time from the remaining duration in the operation.
- If: The new remaining duration is greater than 0.
- Then: Return a modified operation with the reduced duration.
- Else: Return a unit result.
applyOp :: obj -> Float -> Ops obj a -> (obj, Either (Ops obj a) a)
applyOp obj t (Basic (For duration) traversal (To x)) = let
-- (1) update world model values
newObj = obj & traversal %~ updateValue t duration x
-- (2) reduce duration
newDuration = duration - t
-- (3) create new animation/result
result = if newDuration > 0
then Left (Basic (For newDuration) traversal (To x))
else Right ()
in (newObj, result)
This is the updateValue helper function to update a value within the world model. The value is clamped to make sure we don’t overshoot. There might be some numerical instability in the way this is calculated, but I haven’t properly tested this yet.
updateValue ::
Float -> -- time elapsed
Float -> -- duration
Float -> -- target value
Float -> -- current value
Float -- new value
updateValue t duration target current = let
newValue = (current + ((target - current) * t) / duration)
in if target > current
then min target newValue
else max target newValue
We can test this function on a simple example. We will start with (100, 100) as our world model and apply an animation which changes the first value to 150. We end up with a world model of (150, 100) after applying the animation fully, as we expect.
-- our world model
example1_state :: (Float, Float)
example1_state = (100, 100)
-- a basic animation
example1_anim :: Ops (Float, Float) ()
example1_anim = Basic (For 0.2) _1 (To 150)
-- after 1 operation step
example1_1 :: ((Float, Float), Either (Ops (Float, Float) ()) ())
example1_1 = applyOp (example1_state) 0.1 example1_anim
-- ((125.0,100.0),Left Basic (For 0.1) (At ...) (To 150.0))
-- after 2 operation steps
example1_2 :: ((Float, Float), Either (Ops (Float, Float) ()) ())
example1_2 = applyOp (fst example1_1) 0.1 (fromLeft undefined (snd example1_1))
-- ((150.0,100.0),Right ())
Applying Animations
Next, we need to be able to apply a complete animation to a world model. We again take an obj and Float as parameter and a Dsl (Anim obj) a representing the animation. As a result, we obtain the modified world model and animation.
Essentially, how the applyDsl function works is that we apply the operations to the world model and replace the newly obtained animations inside the combinators. If the operations have returned a result when they are finished, we apply their results to the continuation in the combinators.
We take a more in-depth look to the function here. There are three cases to consider:
Bind: We apply the animation within theBindcombinator withapplyOp. This can have two outcomes:- We obtain a result value, we can apply this value to the continuation inside the
Bindcombinator to obtain the new animation. - We obtain a new animation, which replaces the animation in the previous
Bindcombinator.
- We obtain a result value, we can apply this value to the continuation inside the
Par: We apply all of the operations in theParcombinator. Then, we check whether all values after this step areReturnvalues.- If that is the case, we can apply the those values to the continuation within the
Parconstructor. - If that is not the case, we replace the operations inside the
Parcombinator.
- If that is the case, we can apply the those values to the continuation within the
Return: We don’t modify the object or the animation, since the animation is finished.
applyDsl :: obj -> Float -> Dsl (Ops obj) a -> (obj, Dsl (Ops obj) a)
-- (1) Bind case
applyDsl obj t (Bind fa k) = let
(newObj, eResult) = applyOp obj t fa
in case eResult of
Right result -> (newObj, k result)
Left newOp -> (newObj, Bind newOp k)
-- (2) Par case
applyDsl obj t (Par fs k) = let
(newObj, newOps) = applyOps obj t fs
in case returnValues newOps of
Right l -> (newObj, k l)
Left () -> (newObj, Par newOps k)
-- (3) Return case
applyDsl obj t (Return a) = (obj, Return a)
The helper functions applyOps and returnValues are given below. The former applies all the operations in a list to the given world model and keeps track of the final modified world model and new operations. The latter gathers all Return values in a list, but returns Left () if there was a non-Return value.
applyOps :: obj -> Float -> [Dsl (Ops obj) a] -> (obj, [Dsl (Ops obj) a])
applyOps obj t [] = (obj, [])
applyOps obj t (op:r) = let
-- apply first operation
(obj', op') = applyDsl obj t op
-- apply the rest of the operations
(obj'', ops) = applyOps obj' t r
in (obj'', op' : ops)
returnValues :: [Dsl f a] -> Either () [a]
returnValues [] = Right []
returnValues ((Return a):r) = do
l <- returnValues r
return (a : l)
returnValues _ = Left ()
We can take out our tuple world model example again, and apply a simple parallel animation to it to check that it works as we expect.
-- our world model
example2_state :: (Float, Float)
example2_state = (100, 100)
-- a composed animation
example2_anim :: Dsl (Ops (Float, Float)) ()
example2_anim =
par
[ basic (For 0.2) _1 (To 150)
, basic (For 0.2) _2 (To 150)
]
-- after 1 dsl step
example2_1 :: ((Float, Float), Dsl (Ops (Float, Float)) ())
example2_1 = applyDsl example2_state 0.1 example2_anim
-- Note that the 0.2 values inside the animation are reduced to 0.1
{-
( (125.0,125.0)
, Par (
[ Bind (Basic (For 0.1) (At ...) (To 150.0)) (Return)
, Bind (Basic (For 0.1) (At ...) (To 150.0)) (Return)]
) (Return)
)
-}
-- after 2 dsl steps
example2_2 :: ((Float, Float), Dsl (Ops (Float, Float)) ())
example2_2 = applyDsl (fst example2_1) 0.1 (snd example2_1)
-- ((150.0,150.0),Return)
Gluing with Gloss
At this point, we have seen enough to be able to glue everything up to the gloss package and actually create some animations.
First, we will define the representation of our world model in the following data types. The Sprite data type contains a gloss Picture and some additional information on how to draw it. Then we have the collection of sprites in the Sprites data type. And lastly, we have the World data type which contains the sprites and the currently running animations. We also create lenses for all these data types.
data Sprite
= Sprite
{ _x :: Float
, _y :: Float
, _alpha :: Float
, _scale :: Float
, _picture :: Picture
}
makeLenses ''Sprite
data Sprites
= Sprites
{ _box :: Sprite
}
makeLenses ''Sprites
allSprites :: Sprites -> [Sprite]
allSprites (Sprites box) = [box]
data World
= World
{ _sprites :: Sprites
, _runningAnimations :: [Dsl (Ops World) ()]
}
makeLenses ''World
Next, we need various functions which will be passed to the gloss entrypoint. drawSprite takes a Sprite and returns a Picture. The draw function takes a world and creates a picture from it, essentially combining all sprites converted into a Picture into one. The handleInput function will add an animation to the world when the x key is pressed. The update function updates the world model based on the currently running animations. Then we define an initial world model and pass everything into the gloss play function.
drawSprite :: Sprite -> Picture
drawSprite (Sprite {_x, _y, _alpha, _scale, _picture}) =
_picture &
Color (makeColor 1 1 1 _alpha) &
Scale _scale _scale &
Translate _x _y
draw :: World -> Picture
draw (World {_sprites}) = let
worldSprites = allSprites _sprites
in Pictures (map drawSprite worldSprites)
handleInput :: Event -> World -> World
handleInput (EventKey (Char 'x') Down _ _) w@(World {_runningAnimations}) = let
newRAnims = _runningAnimations ++ [fancyBoxAnim]
in w { _runningAnimations = newRAnims }
handleInput _ w = w
update :: Float -> World -> World
update t w@(World {_runningAnimations}) = let
(newWorld, newOps) = applyOps w t _runningAnimations
f (Return _) = False
f _ = True
filteredOps = filter f newOps
in newWorld { _runningAnimations = filteredOps }
boxPic :: Picture
boxPic = Pictures
[ Line [(-1, 1), (1, 1)]
, Line [(1, 1), (1, -1)]
, Line [(1, -1), (-1, -1)]
, Line [(-1, -1), (-1, 1)]
]
initialWorld :: World
initialWorld = let
worldSprites = Sprites (Sprite 0 0 1 20 boxPic)
in World worldSprites []
main :: IO ()
main = let
window = InWindow "animation-dsl" (400, 400) (10, 10)
in play window black 60 initialWorld draw handleInput update
As a last example let’s take a look at a more complicated animation. This animation is similar to the square path animation, but in parallel the box will fade in and out.
fancyBoxAnim = let
fade = seq
[ basic (For 0.125) (sprites . box . alpha) (To 0)
, basic (For 0.125) (sprites . box . alpha) (To 1)
]
in par
[ seqBoxAnim
, seq (replicate 8 fade)
]
Create Effect
So far we have created animations using only the Basic effect. However, there are other interesting effects we can add to the DSL. In this section we will look at the Create effect, which creates an object within the world model.
To add an effect to our DSL, we have to update the Ops data type definition. The Create effect will take as input a function on how to create an object. Then, we also need to know how to access this object later on in the animation, so this function returns an integer index. This index is also the return type of the effect, note that the Create constructor constructs a value of type Anim obj Int. This means that this operation has an Int as result type.
The updated Ops declaration is given below.
data Ops obj a where
Basic :: Duration -> Traversal' obj Float -> To -> Ops obj ()
Create :: (obj -> (obj, Int)) -> Ops obj Int
By adding this constructor, we also have to add a clause to the applyOp function. The implementation is quite easy, we call the create function inside the Create constructor and pass the obtained data along.
applyOp obj t (Create create) = let
(createdObj, objIndex) = create obj
in (createdObj, Right objIndex)
And we can again create a helper function create for convenience.
create :: (obj -> (obj, Int)) -> Dsl (Ops obj) Int
create create = Bind (Create create) (\index -> Return index)
For the following animation we make a small update to our World data type. The _sprites field is now a list of sprites, so it can host a dynamic amount of sprites.
data World
= World
{ _sprites :: [Sprite]
, _runningAnimations :: [Dsl (Ops World) ()]
}
The following animation uses the create effect to create a new box in the world and play a little animation along with it.
createBox :: World -> (World, Int)
createBox w@(World {_sprites}) = let
newIndex = w ^. sprites & length
sprite = Sprite ((-120) + fromIntegral newIndex * 60) 0 0 30 boxPic
newWorld = w { _sprites = _sprites ++ [sprite] }
in (newWorld, newIndex)
atIndex :: Int -> Lens' [a] a
atIndex i = lens (!! i) (\s b -> take i s ++ b : drop (i+1) s)
createBoxAnim :: Dsl (Ops World) ()
createBoxAnim = do
i <- create createBox
par
[ basic (For 0.5) (sprites . atIndex i . alpha) (To 1)
, basic (For 0.5) (sprites . atIndex i . scale) (To 20)
]
This results in the animation below, each new box appearing happens after a key is pressed.

Conclusion
We looked at building an animation DSL from the ground up, starting from a traditional effect handler perspective. We extended this with the Par combinator for parallel animations, created visual animations using the gloss library and added an extra create operation.
One main future direction I want to explore is converting it into a modular effects approach. This allows an end user to mix and match whatever basic effects they want in the DSL. For example, an effect they might want to add is playing sounds during an animation, or maybe hook into game engine primitives such as certain shaders (de)activating. These additional effects can be dependent on how the user wants to use the DSL, and so a modular approach seems appropriate.
Feel free to post any interesting ideas or feedback in the accompanying reddit thread!